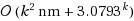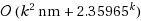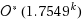| Article ID: | iaor201110813 |
| Volume: | 61 |
| Issue: | 4 |
| Start Page Number: | 817 |
| End Page Number: | 838 |
| Publication Date: | Dec 2011 |
| Journal: | Algorithmica |
| Authors: | Bodlaender L, Heggernes Pinar, Villanger Yngve |
| Keywords: | analysis of algorithms, graphical methods |
We present two parameterized algorithms for the