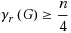Restrained domination in cubic graphs

Let G=(V,E) be a graph. A set S⊆V is a restrained dominating set if every vertex in V-S is adjacent to a vertex in S and to a vertex in V-S. The restrained domination number of G, denoted γ r (G), is the smallest cardinality of a restrained dominating set of G. A graph G is said to be cubic if every vertex has degree three. In this paper, we study restrained domination in cubic graphs. We show that if G is a cubic graph of order n, then 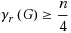${\gamma }_r(G)\ge \frac{n}{4}$ , and characterize the extremal graphs achieving this lower bound. Furthermore, we show that if G is a cubic graph of order n, then ${\gamma }_r(G)\le \frac{5n}{11}$ . Lastly, we show that if G is a claw‐free cubic graph, then γ r (G)=γ(G).