Two uniform machines with nearly equal speeds: unified approach to known sum and known optimum in semi on‐line scheduling

We consider semi on‐line scheduling on two uniform machines. The speed of the slow machine is normalized to 1 while the speed of the fast machine is assumed to be s≥1. Jobs of size J 1,J 2,… arrive one at a time, and each J i (i≥1) has to be assigned to one of the machines before J i+1 arrives. The assignment cannot be changed later. The processing time of the ith job is J i on the slow machine and J i /s on the fast one. The objective is to minimize the makespan. We study both the case where the only information known in advance is the total size Σ i≥1 J i of the jobs and the case where the only information known in advance is the optimum makespan. For each of these two cases, we almost completely determine the best possible competitive ratio of semi on‐line algorithms compared to the off‐line optimum, as a function of s in the range 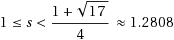$1\le s<\frac{1+\sqrt{17}}{4}\approx 1.2808$ , except for a very short subinterval around s=1.08. We also prove that the best competitive ratio achievable for known optimum is at least as good as the one for known sum, even for any number of uniform machines of any speeds.