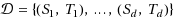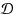An instance of the k
‐generalized connectivity problem consists of an undirected graph G=(V,E), whose edges are associated with non‐negative costs, and a collection
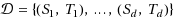 of distinct demands, each of which comprises a pair of disjoint vertex sets. We say that a subgraph ℋ⊆G
connects a demand (S
i
,T
i
) when it contains a path with one endpoint in S
i
and the other in T
i
. Given an integer parameter k, the goal is to identify a minimum cost subgraph that connects at least k demands in
of distinct demands, each of which comprises a pair of disjoint vertex sets. We say that a subgraph ℋ⊆G
connects a demand (S
i
,T
i
) when it contains a path with one endpoint in S
i
and the other in T
i
. Given an integer parameter k, the goal is to identify a minimum cost subgraph that connects at least k demands in
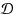 . Alon, Awerbuch, Azar, Buchbinder and Naor (SODA ‘04) seem to have been the first to consider the generalized connectivity paradigm as a unified machinery for incorporating multiple‐choice decisions into network formation settings. Their main contribution in this context was to devise a multiplicative‐update online algorithm for computing log‐competitive fractional solutions, and to propose provably‐good rounding procedures for important special cases. Nevertheless, approximating the generalized connectivity problem in its unconfined form, where one makes no structural assumptions about the underlying graph and collection of demands, has remained an open question up until a recent O(log2
n log2
d) approximation due to Chekuri, Even, Gupta and Segev (SODA ‘08). Unfortunately, the latter result does not extend to connecting a pre‐specified number of demands. Furthermore, even the simpler case of singleton demands has been established as a challenging computational task, when Hajiaghayi and Jain (SODA ‘06) related its inapproximability to that of dense
k
‐subgraph. In this paper, we present the first non‐trivial approximation algorithm for k‐generalized connectivity, which is derived by synthesizing several techniques originating in probabilistic embeddings of finite metrics, network design, and randomization. Specifically, our algorithm constructs, with constant probability, a feasible subgraph whose cost is within a factor of O(n
2/3·polylog(n,k)) of optimal. We believe that the fundamental approach illustrated in the current writing is of independent interest, and may be applicable in other settings as well.
. Alon, Awerbuch, Azar, Buchbinder and Naor (SODA ‘04) seem to have been the first to consider the generalized connectivity paradigm as a unified machinery for incorporating multiple‐choice decisions into network formation settings. Their main contribution in this context was to devise a multiplicative‐update online algorithm for computing log‐competitive fractional solutions, and to propose provably‐good rounding procedures for important special cases. Nevertheless, approximating the generalized connectivity problem in its unconfined form, where one makes no structural assumptions about the underlying graph and collection of demands, has remained an open question up until a recent O(log2
n log2
d) approximation due to Chekuri, Even, Gupta and Segev (SODA ‘08). Unfortunately, the latter result does not extend to connecting a pre‐specified number of demands. Furthermore, even the simpler case of singleton demands has been established as a challenging computational task, when Hajiaghayi and Jain (SODA ‘06) related its inapproximability to that of dense
k
‐subgraph. In this paper, we present the first non‐trivial approximation algorithm for k‐generalized connectivity, which is derived by synthesizing several techniques originating in probabilistic embeddings of finite metrics, network design, and randomization. Specifically, our algorithm constructs, with constant probability, a feasible subgraph whose cost is within a factor of O(n
2/3·polylog(n,k)) of optimal. We believe that the fundamental approach illustrated in the current writing is of independent interest, and may be applicable in other settings as well.