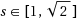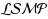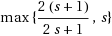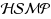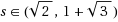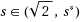Semi‐online scheduling on two uniform machines with the known largest size

This paper investigates semi‐online scheduling on two uniform machines with the known largest size. Denote by s j the speed of each machine, j=1,2. Assume 0<s 1≤s 2, and let s=s 2/s 1 be the speed ratio. First, for the speed ratio 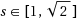$s\in [1,\sqrt{2}]$ , we present an optimal semi‐online algorithm 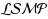$\mathrm{ℒ𝒮ℳ𝒫}$ with the competitive ratio 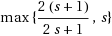$\max \{\frac{2(s+1)}{2s+1},s\}$ . Second, we present a semi‐online algorithm 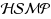$\mathrm{\mathscr{H}𝒮ℳ𝒫}$ . And for 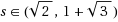$s\in (\sqrt{2}\mathrm{,1}+\sqrt{3})$ , the competitive ratio of 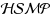$\mathrm{\mathscr{H}𝒮ℳ𝒫}$ is strictly smaller than that of the online algorithm $\mathrm{ℒ𝒮}$ . Finally, for the speed ratio s≥s ^*≈3.715, we show that the known largest size cannot help us to design a semi‐online algorithm with the competitive ratio strictly smaller than that of 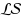$\mathrm{ℒ𝒮}$ . 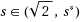Moreover, we show a lower bound for $s\in (\sqrt{2},s^{*})$ .