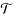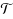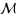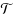Let G=(V,E) be a connected graph such that each edge e∈E is weighted by a nonnegative real w(e). Let s be a vertex designated as a sink, M⊆V be a set of terminals with a demand function q:M→R +, κ>0 be a routing capacity, and λ≥1 be an integer edge capacity. The capacitated tree‐routing problem (CTR) asks to find a partition
={Z1,Z2,…,Z 𝓁 } of M and a set
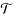= {T1, T2, … T𝓁} of trees of G such that each Ti contains Zi⋃{s} and satisfies Σ v ∈ Ziq(v)≤κ. A single copy of an edge ϵ∈E can be shared by at most λ trees in
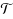; any integer number of copies of e are allowed to be installed, where the cost of installing a copy of e is w(e). The objective is to find a solution
(
,
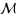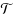) that minimizes the total installing cost. In this paper, we propose a (2+ρ ST )‐approximation algorithm to CTR, where ρ ST is any approximation ratio achievable for the Steiner tree problem.
