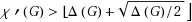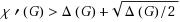Approximating the chromatic index of multigraphs

It is well known that if G is a multigraph then χ′(G)≥χ′^*(G)≔ max {Δ(G),Γ(G)}, where χ′(G) is the chromatic index of G, χ′^*(G) is the fractional chromatic index of G, Δ(G) is the maximum degree of G, and Γ(G)=max{2|E(G[U])|/(|U|−1):U⊆V(G),|U|≥3, |U| is odd}. The conjecture that χ′(G)≤max {Δ,(G)+1,⌈Γ(G)⌉} was made independently by Goldberg (Discret. Anal. 23:3–7, 1973), Anderson (Math. Scand. 40:161–175, 1977), and Seymour (Proc. Lond. Math. Soc. 38:423–460, 1979). Using a probabilistic argument Kahn showed that for any c>0 there exists D>0 such that χ′(G)≤χ′^*(G)+c χ′^*(G) when χ′^*(G)>D. Nishizeki and Kashiwagi proved this conjecture for multigraphs G with χ′(G)>⌊(11Δ(G)+8)/10⌋; and Scheide recently improved this bound to χ′(G)>⌊(15Δ(G)+12)/14⌋. We prove this conjecture for multigraphs G with 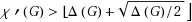$\chi \prime (G)>\lfloor \Delta (G)+\sqrt{\Delta (G)/2}\rfloor$ , improving the above mentioned results. As a consequence, for multigraphs G with 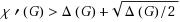$\chi \prime (G)>\Delta (G)+\sqrt{\Delta (G)/2}$ the answer to a 1964 problem of Vizing is in the affirmative.