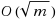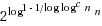Approximation and hardness results for label cut and related problems

We investigate a natural combinatorial optimization problem called the Label Cut problem. Given an input graph G with a source s and a sink t, the edges of G are classified into different categories, represented by a set of labels. The labels may also have weights. We want to pick a subset of labels of minimum cardinality (or minimum total weight), such that the removal of all edges with these labels disconnects s and t. We give the first non‐trivial approximation and hardness results for the Label Cut problem. Firstly, we present an 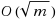$O(\sqrt{m})$ ‐approximation algorithm for the Label Cut problem, where m is the number of edges in the input graph. Secondly, we show that it is NP‐hard to approximate Label Cut within 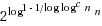$2^{{\log }^{1‐1/\log {\log }^{c}n}n}$ for any constant c<1/2, where n is the input length of the problem. Thirdly, our techniques can be applied to other previously considered optimization problems. In particular we show that the Minimum Label Path problem has the same approximation hardness as that of Label Cut, simultaneously improving and unifying two known hardness results for this problem which were previously the best (but incomparable due to different complexity assumptions).