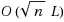An O(√nL) iteration primal‐dual second‐order corrector algorithm for linear programming

In this paper, we propose a primal‐dual second‐order corrector interior point algorithm for linear programming problems. At each iteration, the method computes a corrector direction in addition to the Ai–Zhang direction (Ai and Zhang, 2005), in an attempt to improve performance. The corrector is multiplied by the square of the step‐size in the expression of the new iterate. We prove that the use of the corrector step does not cause any loss in the worst‐case complexity of the algorithm. To our best knowledge, this is the first wide neighborhood second‐order corrector algorithm enjoyed the low iteration bound of $O(\sqrt{n}L)$ , the same as the best known complexity results for interior point methods.