Scheduling two agents on uniform parallel machines with makespan and cost functions

We consider the problem of scheduling two jobs A and B on a set of m uniform parallel machines. Each job is assumed to be independent from the other: job A and job B are made up of n A and n B operations, respectively. Each operation is defined by its processing time and possibly additional data such as a due date, a weight, etc., and must be processed on a single machine. All machines are uniform, i.e. each machine has its own processing speed. Notice that we consider the special case of equal‐size operations, i.e. all operations have the same processing time. The scheduling of operations of job A must be achieved to minimize a general cost function F ^A , whereas it is the makespan that must be minimized when scheduling the operations of job B. These kind of problems are called multiple agent scheduling problems. As we are dealing with two conflicting criteria, we focus on the calculation of strict Pareto optima for F ^A and 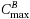$C_{\max }^B$ criteria. In this paper we consider different min‐max and min‐sum versions of function F ^A and provide special properties as well as polynomial time algorithms.