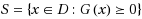Consider a convex set
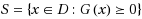 , where G(x) is a symmetric matrix whose every entry is a polynomial or rational function, 𝒟 ⊆ ℝ
n
is a domain on which G(x) is defined, and
, where G(x) is a symmetric matrix whose every entry is a polynomial or rational function, 𝒟 ⊆ ℝ
n
is a domain on which G(x) is defined, and
 means G(x) is positive semidefinite. The set S is called semidefinite representable if it equals the projection of a higher dimensional set that is defined by a linear matrix inequality (LMI). This paper studies sufficient conditions guaranteeing semidefinite representability of S. We prove that S is semidefinite representable in the following cases: (i) 𝒟=ℝ
n
, G(x) is a matrix polynomial and matrix sos‐concave; (ii) 𝒟 is compact convex, G(x) is a matrix polynomial and strictly matrix concave on 𝒟 (iii) G(x) is a matrix rational function and q‐module matrix concave on 𝒟. Explicit constructions of semidefinite representations are given. Some examples are illustrated.
means G(x) is positive semidefinite. The set S is called semidefinite representable if it equals the projection of a higher dimensional set that is defined by a linear matrix inequality (LMI). This paper studies sufficient conditions guaranteeing semidefinite representability of S. We prove that S is semidefinite representable in the following cases: (i) 𝒟=ℝ
n
, G(x) is a matrix polynomial and matrix sos‐concave; (ii) 𝒟 is compact convex, G(x) is a matrix polynomial and strictly matrix concave on 𝒟 (iii) G(x) is a matrix rational function and q‐module matrix concave on 𝒟. Explicit constructions of semidefinite representations are given. Some examples are illustrated.