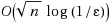A polynomial arc‐search interior‐point algorithm for convex quadratic programming

Arc‐search is developed for linear programming in . The algorithms search for optimizers along an ellipse that is an approximation of the central path. In this paper, the arc‐search method is applied to primal–dual path‐following interior‐point method for convex quadratic programming. A simple algorithm with iteration complexity 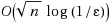$O\left(\sqrt{n}\log (1/ϵ)\right)$ is devised. Several improvements on the simple algorithm, which improve computational efficiency, increase step length, and further reduce duality gap in every iteration, are then proposed and implemented. It is intuitively clear that the iteration with these improvements will reduce the duality gap more than the iteration of the simple algorithm without the improvements, though it is hard to show how much these improvements reduce the complexity bound. The proposed algorithm is implemented in MATLAB and tested on quadratic programming problems originating from . The result is compared to the one obtained by LOQO in . The proposed algorithm uses fewer iterations in all these problems and the number of total iterations is 27% fewer than the one obtained by LOQO. This preliminary result shows that the proposed algorithm is promising.