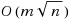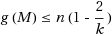Bounded Unpopularity Matchings

We investigate the following problem: given a set of jobs and a set of people with preferences over the jobs, what is the optimal way of matching people to jobs? Here we consider the notion of popularity. A matching M is popular if there is no matching M′ such that more people prefer M′ to M than the other way around. Determining whether a given instance admits a popular matching and, if so, finding one, was studied by Abraham et al. (2007). If there is no popular matching, a reasonable substitute is a matching whose unpopularity is bounded. We consider two measures of unpopularity–unpopularity factor denoted by u(M) and unpopularity margin denoted by g(M). McCutchen recently showed that computing a matching M with the minimum value of u(M) or g(M) is NP‐hard, and that if G does not admit a popular matching, then we have u(M)≥2 for all matchings M in G. Here we show that a matching M that achieves u(M)=2 can be computed in 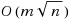$O(m\sqrt{n})$ time (where m is the number of edges in G and n is the number of nodes) provided a certain graph H admits a matching that matches all people. We also describe a sequence of graphs: H=H 2,H 3,…,H k such that if H k admits a matching that matches all people, then we can compute in $O(\mathrm{km}\sqrt{n})$ time a matching M such that u(M)≤k-1 and $g(M)\le n(1‐\frac{2}{k})$ . 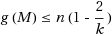Simulation results suggest that our algorithm finds a matching with low unpopularity in random instances.