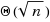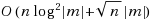We address the problem of minimizing power consumption when broadcasting a message from one node to all the other nodes in a radio network. To enable power savings for such a problem, we introduce a compelling new data streaming problem which we call the
Bad Santa problem. Our results on this problem apply for any situation where: (1) a node can listen to a set of
n nodes, out of which at least half are non‐faulty and know the correct message; and (2) each of these
n nodes sends according to some predetermined schedule which assigns each of them its own unique time slot. In this situation, we show that in order to receive the correct message with probability 1, it is necessary and sufficient for the listening node to listen to a
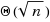 expected number of time slots. Moreover, if we allow for repetitions of transmissions so that each sending node sends the message
O(log
*
n) times (i.e. in
O(log
*
n) rounds each consisting of the
n time slots), then listening to
O(log
*
n) expected number of time slots suffices. We show that this is near optimal. We describe an application of our result to the popular grid model for a radio network. Each node in the network is located on a point in a two dimensional grid, and whenever a node sends a message
m, all awake nodes within
L
∞ distance
r receive
m. In this model, up to
expected number of time slots. Moreover, if we allow for repetitions of transmissions so that each sending node sends the message
O(log
*
n) times (i.e. in
O(log
*
n) rounds each consisting of the
n time slots), then listening to
O(log
*
n) expected number of time slots suffices. We show that this is near optimal. We describe an application of our result to the popular grid model for a radio network. Each node in the network is located on a point in a two dimensional grid, and whenever a node sends a message
m, all awake nodes within
L
∞ distance
r receive
m. In this model, up to
 nodes within any 2
r+1 by 2
r+1 square in the grid can suffer Byzantine faults. Moreover, we assume that the nodes that suffer Byzantine faults are chosen and controlled by an adversary that knows everything except for the random bits of each non‐faulty node. This type of adversary models worst‐case behavior due to malicious attacks on the network; mobile nodes moving around in the network; or static nodes losing power or ceasing to function. Let
n=
r(2
r+1). We show how to solve the broadcast problem in this model with each node sending and receiving an expected
nodes within any 2
r+1 by 2
r+1 square in the grid can suffer Byzantine faults. Moreover, we assume that the nodes that suffer Byzantine faults are chosen and controlled by an adversary that knows everything except for the random bits of each non‐faulty node. This type of adversary models worst‐case behavior due to malicious attacks on the network; mobile nodes moving around in the network; or static nodes losing power or ceasing to function. Let
n=
r(2
r+1). We show how to solve the broadcast problem in this model with each node sending and receiving an expected
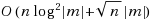 bits where |
m| is the number of bits in
m, and, after broadcasting a fingerprint of
m, each node is awake only an expected
bits where |
m| is the number of bits in
m, and, after broadcasting a fingerprint of
m, each node is awake only an expected
 time slots. Moreover, for
t≤(1-
ϵ)(
r/2)(2
r+1), for any constant
ϵ>0, we can achieve an even better energy savings. In particular, if we allow each node to send
O(log
*
n) times, we achieve reliable broadcast with each node sending
O(
nlog
2|
m|+(log
*
n)|
m|) bits and receiving an expected
O(
nlog
2|
m|+(log
*
n)|
m|) bits and, after broadcasting a fingerprint of
m, each node is awake for only an expected
O(log
*
n) time slots. Our results compare favorably with previous protocols that required each node to send Θ(|
m|) bits, receive Θ(
n|
m|) bits and be awake for Θ(
n) time slots.
time slots. Moreover, for
t≤(1-
ϵ)(
r/2)(2
r+1), for any constant
ϵ>0, we can achieve an even better energy savings. In particular, if we allow each node to send
O(log
*
n) times, we achieve reliable broadcast with each node sending
O(
nlog
2|
m|+(log
*
n)|
m|) bits and receiving an expected
O(
nlog
2|
m|+(log
*
n)|
m|) bits and, after broadcasting a fingerprint of
m, each node is awake for only an expected
O(log
*
n) time slots. Our results compare favorably with previous protocols that required each node to send Θ(|
m|) bits, receive Θ(
n|
m|) bits and be awake for Θ(
n) time slots.