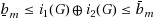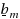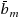Using size for bounding expressions of graph invariants

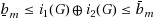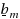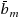With the help of the AutoGraphiX system, we study relations of the form ${\underset{¯}{b}}_m\le i_1\left(G\right)\oplus i_2\left(G\right)\le {\overline{b}}_m$ where i1(G) and i2(G) are invariants of the graph G, ⊕ is one of the operations −,+,/,×, ${\underset{¯}{b}}_m$ and ${\overline{b}}_m$ are best possible lower and upper bounding functions depending only one the size m of G. Specifically, we consider pairs of indices where i 1(G) is a measure of distance, i.e., diameter, radius or average eccentricity, and i 2(G) is a measure of connectivity, i.e., minimum degree, edge connectivity and vertex connectivity. Conjectures are obtained and then proved in almost all cases.