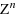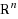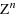| Article ID: | iaor20117345 |
| Volume: | 214 |
| Issue: | 3 |
| Start Page Number: | 493 |
| End Page Number: | 500 |
| Publication Date: | Nov 2011 |
| Journal: | European Journal of Operational Research |
| Authors: | Talman Dolf, Yang Zaifu, van der Laan Gerard |
We study the existence problem of a zero point of a function defined on a finite set of elements of the integer lattice