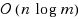We consider the problem of scheduling n intervals (jobs with fixed starting times) on m machines with different speeds with the objective to maximize the number of accepted intervals. We prove that the offline version of the problem is strongly NP‐hard to solve. For the online version, we show a lower bound of
 on the competitive ratio of any deterministic online algorithm for the problem. Moreover, we present two simple greedy rules for online algorithms and show that any online algorithm using these rules is 2‐competitive. One of these 2‐competitive algorithms is shown to run in
on the competitive ratio of any deterministic online algorithm for the problem. Moreover, we present two simple greedy rules for online algorithms and show that any online algorithm using these rules is 2‐competitive. One of these 2‐competitive algorithms is shown to run in
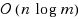 time. Additionally, we prove that our greedy rules impose no loss in the sense that every online algorithm for the problem can be modified to use the rules without reducing the number of accepted intervals on any instance.
time. Additionally, we prove that our greedy rules impose no loss in the sense that every online algorithm for the problem can be modified to use the rules without reducing the number of accepted intervals on any instance.