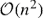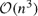| Article ID: | iaor20118124 |
| Volume: | 61 |
| Issue: | 2 |
| Start Page Number: | 402 |
| End Page Number: | 418 |
| Publication Date: | Oct 2011 |
| Journal: | Algorithmica |
| Authors: | Wang Yue-Li, Chang Jou-Ming, Kao Kuo-Hua, Juan Su-Tzu |
| Keywords: | networks: path |
Given an edge‐weighted undirected graph