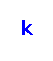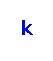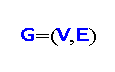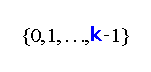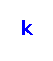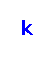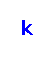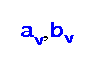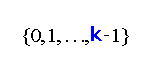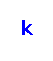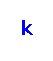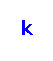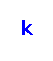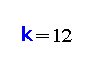On compact k‐edge‐colorings: A polynomial time reduction from linear to cyclic

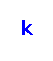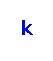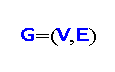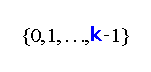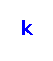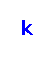A $k$ ‐edge‐coloring of a graph $G=(V,E)$ is a function $c$ that assigns an integer $c\left(e\right)$ (called color) in $\{0,1,\dots ,k‐1\}$ to every edge $e\in E$ so that adjacent edges get different colors. A $k$ ‐edge‐coloring is linear compact if the colors on the edges incident to every vertex are consecutive. The problem $k$ ‐ $LCCP$ is to determine whether a given graph admits a linear compact $k$ ‐edge coloring. 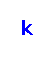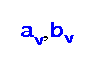A $k$ ‐edge‐coloring is cyclic compact if for every vertex $v$ there are two positive integers $a_v,b_v$ in $\{0,1,\dots ,k‐1\}$ such that the colors on the edges incident to 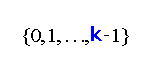$v$ are exactly $\{a_v,(a_v+1)\text{mod}k,\dots ,b_v\}$ . 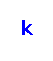The problem $k$ ‐ $CCCP$ is to determine whether a given graph admits a cyclic compact $k$ ‐edge coloring. 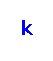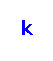We show that the $k$ ‐ $LCCP$ with possibly imposed or forbidden colors on some edges is polynomially reducible to the 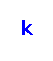$k$ ‐ $CCCP$ when $k=12$ , and to the 12‐ 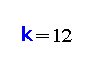$CCCP$ when $k<12$ .