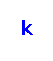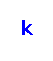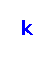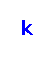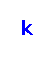| Article ID: | iaor20117113 |
| Volume: | 8 |
| Issue: | 3 |
| Start Page Number: | 478 |
| End Page Number: | 494 |
| Publication Date: | Aug 2011 |
| Journal: | Discrete Optimization |
| Authors: | Januschowski Tim, Pfetsch Marc E |
| Keywords: | programming: integer |
Given an undirected node‐weighted graph and a positive integer