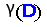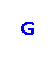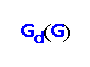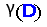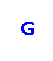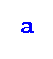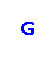| Article ID: | iaor20117111 |
| Volume: | 8 |
| Issue: | 3 |
| Start Page Number: | 452 |
| End Page Number: | 458 |
| Publication Date: | Aug 2011 |
| Journal: | Discrete Optimization |
| Authors: | Caro Yair, Henning Michael A |
| Keywords: | graph partitioning, greedy algorithms |
A directed dominating set in a directed graph