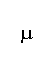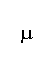| Article ID: | iaor20117109 |
| Volume: | 8 |
| Issue: | 3 |
| Start Page Number: | 428 |
| End Page Number: | 445 |
| Publication Date: | Aug 2011 |
| Journal: | Discrete Optimization |
| Authors: | Hirai Hiroshi, Koichi Shungo |
| Keywords: | combinatorial optimization, location |
In this paper we address a topological approach to multiflow (multicommodity flow) problems in directed networks. Given a terminal weight