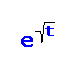Uniform approximations for the M/G/1 queue with subexponential processing times

This paper studies the asymptotic behavior of the steady‐state waiting time, W ∞, of the M/G/1 queue with Subexponential processing times for different combinations of traffic intensities and overflow levels. In particular, we provide insights into the regions of large deviations where the so‐called heavy‐traffic approximation and heavy‐tail asymptotic hold. For queues whose service time distribution decays slower than 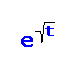$e^{‐\sqrt{t}}$ we identify a third region of asymptotics where neither the heavy‐traffic nor the heavy‐tail approximations are valid. These results are obtained by deriving approximations for P(W ∞>x) that are either uniform in the traffic intensity as the tail value goes to infinity or uniform on the positive axis as the traffic intensity converges to one. Our approach makes clear the connection between the asymptotic behavior of the steady‐state waiting time distribution and that of an associated random walk.