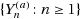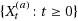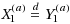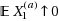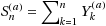| Article ID: | iaor20115774 |
| Volume: | 67 |
| Issue: | 4 |
| Start Page Number: | 295 |
| End Page Number: | 304 |
| Publication Date: | Apr 2011 |
| Journal: | Queueing Systems |
| Authors: | Kosinski K M, Boxma O J, Zwart B |
| Keywords: | Levy-stable processes |
In this paper we derive a technique for obtaining limit theorems for suprema of Lévy processes from their random walk counterparts. For each