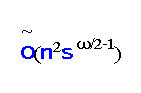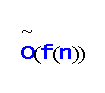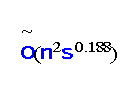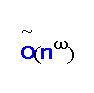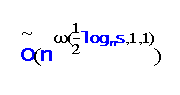We use randomness to exploit the potential sparsity of the Boolean matrix product in order to speed up the computation of the product. Our new fast output‐sensitive algorithm for Boolean matrix product and its witnesses is randomized and provides the Boolean product and its witnesses almost certainly. Its worst‐case time performance is expressed in terms of the input size and the number of non‐zero entries of the product matrix. It runs in time
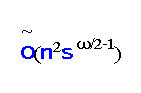 , where the input matrices have size n×n, the number of non‐zero entries in the product matrix is at most s, ω is the exponent of the fast matrix multiplication and
, where the input matrices have size n×n, the number of non‐zero entries in the product matrix is at most s, ω is the exponent of the fast matrix multiplication and
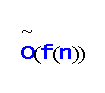 denotes O(f(n)log
d
n) for some constant d. By the currently best bound on ω, its running time can be also expressed as
denotes O(f(n)log
d
n) for some constant d. By the currently best bound on ω, its running time can be also expressed as
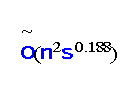 . Our algorithm is substantially faster than the output‐sensitive column‐row method for Boolean matrix product for s larger than n
1.232 and it is never slower than the fast
. Our algorithm is substantially faster than the output‐sensitive column‐row method for Boolean matrix product for s larger than n
1.232 and it is never slower than the fast
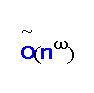 ‐time algorithm for this problem. By applying the fast rectangular matrix multiplication, we can refine our upper bound further to the form
‐time algorithm for this problem. By applying the fast rectangular matrix multiplication, we can refine our upper bound further to the form
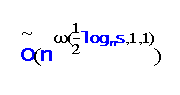 , where ω(p,q,t) is the exponent of the fast multiplication of an n
p
×n
q
matrix by an n
q
×n
t
matrix. We also present a partial derandomization of our algorithm as well as its generalization to include the Boolean product of rectangular Boolean matrices. Finally, we show several applications of our output‐sensitive algorithms.
, where ω(p,q,t) is the exponent of the fast multiplication of an n
p
×n
q
matrix by an n
q
×n
t
matrix. We also present a partial derandomization of our algorithm as well as its generalization to include the Boolean product of rectangular Boolean matrices. Finally, we show several applications of our output‐sensitive algorithms.