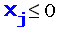| Article ID: | iaor20115239 |
| Volume: | 39 |
| Issue: | 3 |
| Start Page Number: | 198 |
| End Page Number: | 199 |
| Publication Date: | May 2011 |
| Journal: | Operations Research Letters |
| Authors: | Gnlk Oktay, Dash Sanjeeb, Raack Christian |
| Keywords: | cutting plane algorithms, polyhedra, relaxation methods |
Anderson et al. (2005) show that for a polyhedral mixed integer set defined by a constraint system