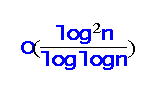The Directed Orienteering Problem

This paper studies vehicle routing problems on asymmetric metrics. Our starting point is the directed k‐TSP problem: given an asymmetric metric (V,d), a root r∈V and a target k≤|V|, compute the minimum length tour that contains r and at least k other vertices. We present a polynomial time $O(\frac{{\log }^{2}n}{\log \log n}\cdot \log k)$ ‐approximation algorithm for this problem. 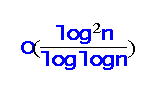We use this algorithm for directed k‐TSP to obtain an $O(\frac{{\log }^{2}n}{\log \log n})$ ‐approximation algorithm for the directed orienteering problem. This answers positively, the question of poly‐logarithmic approximability of directed orienteering, an open problem from Blum et al. (2007). The previously best known results were quasi‐polynomial time algorithms with approximation guarantees of O(log ² k) for directed k‐TSP, and O(log n) for directed orienteering (2005). Using the algorithm for directed orienteering within the framework of Blum et al. (2007) and Bansal et al. (2004), we also obtain poly‐logarithmic approximation algorithms for the directed versions of discounted‐reward TSP and vehicle routing problem with time‐windows.