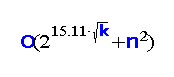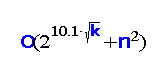Planar Feedback Vertex Set and Face Cover: Combinatorial Bounds and Subexponential Algorithms

The Planar Feedback Vertex Set problem asks whether an n‐vertex planar graph contains at most k vertices meeting all its cycles. The Face Cover problem asks whether all vertices of a plane graph G lie on the boundary of at most k faces of G. Standard techniques from parameterized algorithm design indicate that both problems can be solved by sub‐exponential parameterized algorithms (where k is the parameter). In this paper we improve the algorithmic analysis of both problems by proving a series of combinatorial results relating the branchwidth of planar graphs with their face cover. Combining this fact with duality properties of branchwidth, allows us to derive analogous results on feedback vertex set. 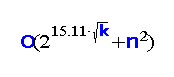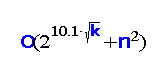As a consequence, it follows that Planar Feedback Vertex Set and Face Cover can be solved in $O(2^{15.11\cdot \sqrt{k}}+n^2)$ and $O(2^{10.1\cdot \sqrt{k}}+n^2)$ steps, respectively.