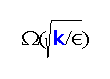A coloring of a graph is convex if it induces a partition of the vertices into connected subgraphs. Besides being an interesting property from a theoretical point of view, tests for convexity have applications in various areas involving large graphs. We study the important subcase of testing for convexity in trees. This problem is linked, among other possible applications, with the study of phylogenetic trees, which are central in genetic research, and are used in linguistics and other areas. We give a 1‐sided, non‐adaptive, distribution‐free ϵ‐test for the convexity of tree colorings. The query complexity of our test is O(k/ϵ), where k is the number of colors, and the additional computational complexity is O(n). On the other hand, we prove a lower bound of
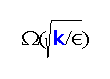on the query complexity of tests for convexity in the standard model, which applies even for (unweighted) paths. We also consider whether the dependency on k can be reduced in some cases, and provide an alternative testing algorithm for the case of paths. Then we investigate a variant of convexity, namely quasi‐convexity, in which all but one of the colors are required to induce connected components. For this problem we provide a 1‐sided, non‐adaptive ϵ‐test with query complexity O(k/ϵ
2) and time complexity O(kn/ϵ). For both our convexity and quasi‐convexity tests, we show that, assuming that a query takes constant time, the time complexity can be reduced to a constant independent of n if we allow a preprocessing stage of time O(n) and O(n
2), respectively. Finally, we show how to test for a variation of convexity and quasi‐convexity where the maximum number of connectivity classes of each color is allowed to be a constant value other than 1.
