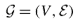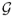Power optimization is a central issue in wireless network design. Given a graph with costs on the edges, the power of a node is the maximum cost of an edge incident to it, and the power of a graph is the sum of the powers of its nodes. Motivated by applications in wireless networks, we consider several fundamental undirected network design problems under the power minimization criteria. Given a graph
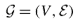 with edge costs {c(e):e∈ℰ} and degree requirements {r(v):v∈V}, the Minimum-Power Edge-Multi-Cover (MPEMC) problem is to find a minimum‐power subgraph G of
with edge costs {c(e):e∈ℰ} and degree requirements {r(v):v∈V}, the Minimum-Power Edge-Multi-Cover (MPEMC) problem is to find a minimum‐power subgraph G of
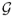 so that the degree of every node v in G is at least r(v). We give an O(log n)‐approximation algorithms for MPEMC , improving the previous ratio O(log 4
n). This is used to derive an O(log n+α)‐approximation algorithm for the undirected Minimum-Power k -Connected Subgraph (MPkCS) problem, where α is the best known ratio for the min‐cost variant of the problem. Currently,
so that the degree of every node v in G is at least r(v). We give an O(log n)‐approximation algorithms for MPEMC , improving the previous ratio O(log 4
n). This is used to derive an O(log n+α)‐approximation algorithm for the undirected Minimum-Power k -Connected Subgraph (MPkCS) problem, where α is the best known ratio for the min‐cost variant of the problem. Currently,
 which is O(log k) unless k=n-o(n), and is O(log 2
k)=O(log 2
n) for k=n-o(n). Our result shows that the min‐power and the min‐cost versions of the
problem are equivalent with respect to approximation, unless the min‐cost variant admits an o(log n)‐approximation, which seems to be out of reach at the moment.
which is O(log k) unless k=n-o(n), and is O(log 2
k)=O(log 2
n) for k=n-o(n). Our result shows that the min‐power and the min‐cost versions of the
problem are equivalent with respect to approximation, unless the min‐cost variant admits an o(log n)‐approximation, which seems to be out of reach at the moment.