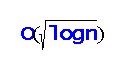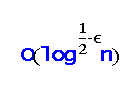Approximability of Packing Disjoint Cycles

Given a graph G, the edge‐disjoint cycle packing problem is to find the largest set of cycles of which no two share an edge. For undirected graphs, the best known approximation algorithm has ratio 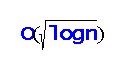$O(\sqrt{\log n})$ (Krivelevich et al, 2009). In fact, they proved the same upper bound for the integrality gap of this problem by presenting a simple greedy algorithm. Here we show that this is almost best possible. By modifying integrality gap and hardness results for the edge‐disjoint paths problem (Andrews et al, 2005; Chuzhoy and Khanna , 2005), we show that the undirected edge‐disjoint cycle packing problem is quasi‐NP‐hard to approximate within ratio of 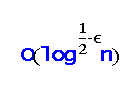$O({\log }^{\frac{1}{2}‐\epsilon }n)$ for any constant ϵ>0. The same result holds for the problem of packing vertex‐disjoint cycles.