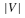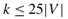Exact Algorithms for Cluster Editing: Evaluation and Experiments

The Cluster Editing problem is defined as follows: Given an undirected, loopless graph, we want to find a set of edge modifications (insertions and deletions) of minimum cardinality, such that the modified graph consists of disjoint cliques. We present empirical results for this problem using exact methods from fixed‐parameter algorithmics and linear programming. We investigate parameter‐independent data reduction methods and find that effective preprocessing is possible if the number of edge modifications k is smaller than some multiple of 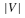$lvertV\mathrm{vert}$ , where V is the vertex set of the input graph. In particular, combining parameter‐dependent data reduction with lower and upper bounds we can effectively reduce graphs satisfying 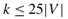$k\le 25lvertV\mathrm{vert}$ . In addition to the fastest known fixed‐parameter branching strategy for the problem, we investigate an integer linear program (ILP) formulation of the problem using a cutting plane approach. Our results indicate that both approaches are capable of solving large graphs with 1000 vertices and several thousand edge modifications. For the first time, complex and very large graphs such as biological instances allow for an exact solution, using a combination of the above techniques.