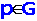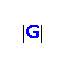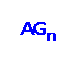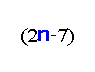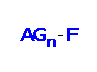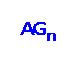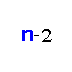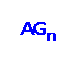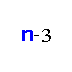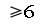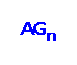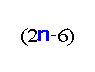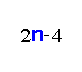Fault tolerance of vertex pancyclicity in alternating group graphs

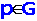We study fault tolerance of vertex k pancyclicity of the alternating group graph ${\mathit{AG}}_n$ . A graph G is vertex k pancyclic, if for every vertex $p\in G$ , there is a cycle going through p of every length from k to 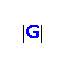$|G|$ . Xue and Liu [Z.‐J. Xue, S.‐Y. Liu, An optimal result on fault‐tolerant cycle‐embedding in alternating group graphs, Inform. Proc. Lett. 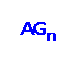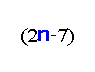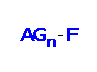109 (2009) 1197–1201] put the conjecture that ${\mathit{AG}}_n$ is $(2n‐7)$ ‐fault‐tolerant vertex pancyclic, which means that if the number of faults $|F|\le 2n‐7$ , then ${\mathit{AG}}_n‐F$ is still vertex pancyclic. Chang and Yang [J.‐M. Chang, J.‐S. Yang, Fault‐tolerant cycle‐embedding in alternating group graphs, Appl. Math. Comput. 197 (2008) 760–767] showed that for the shortest cycles the fault‐tolerance of 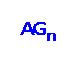${\mathit{AG}}_n$ is much lower. They noted that with 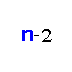$n‐2$ faults one can cut all 3‐cycles going through a given vertex p (it is easy to observe that the same set of faults cuts all 4‐ and 5‐cycles going through p). 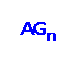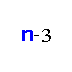On the other hand they show that ${\mathit{AG}}_n$ is $n‐3$ ‐fault tolerant vertex 3 pancyclic. In this paper we show that the cycles of length 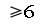$\ge 6$ are much more fault‐tolerant. 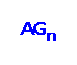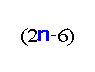More precisely, we show that ${\mathit{AG}}_n$ is $(2n‐6)$ ‐fault‐tolerant vertex 6 pancyclic. This bound is optimal, because every vertex p has 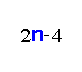$2n‐4$ neighbors.