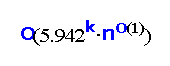| Article ID: | iaor20112721 |
| Volume: | 8 |
| Issue: | 1 |
| Start Page Number: | 97 |
| End Page Number: | 109 |
| Publication Date: | Feb 2011 |
| Journal: | Discrete Optimization |
| Authors: | Raman Venkatesh, Lokshtanov Daniel, Saurabh Saket, Sikdar Somnath |
| Keywords: | complexity, minimum spanning tree |
We study the parameterized complexity of a directed analog of the