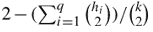Tight Approximation Ratio of a General Greedy Splitting Algorithm for the Minimum k‐Way Cut Problem

For an edge‐weighted connected undirected graph, the minimum k‐way cut problem is to find a subset of edges of minimum total weight whose removal separates the graph into k connected components. The problem is NP‐hard when k is part of the input and W[1]‐hard when k is taken as a parameter. A simple algorithm for approximating a minimum k‐way cut is to iteratively increase the number of components of the graph by h-1, where 2≤h≤k, until the graph has k components. The approximation ratio of this algorithm is known for h≤3 but is open for h≥4. In this paper, we consider a general algorithm that successively increases the number of components of the graph by h i -1, where 2≤h 1≤h 2≤…≤h q and Σ i=1 ^q (h i -1)=k-1. We prove that the approximation ratio of this general 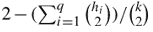algorithm is $2‐({\Sigma }_{i=1}^q{h}_{i}choose2)/kchoose2$ , which is tight. Our result implies that the approximation ratio of the simple iterative algorithm is 2-h/k+O(h ²/k ²) in general and 2-h/k if k-1 is a multiple of h-1.