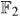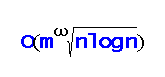We consider the problem of computing an approximate minimum cycle basis of an undirected non‐negative edge‐weighted graph G with m edges and n vertices; the extension to directed graphs is also discussed. In this problem, a {0,1} incidence vector is associated with each cycle and the vector space over
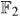 generated by these vectors is the cycle space of G. A set of cycles is called a cycle basis of G if it forms a basis for its cycle space. A cycle basis where the sum of the weights of the cycles is minimum is called a minimum cycle basis of G. Cycle bases of low weight are useful in a number of contexts, e.g. the analysis of electrical networks, structural engineering, chemistry, and surface reconstruction. Although in most such applications any cycle basis can be used, a low weight cycle basis often translates to better performance and/or numerical stability. Despite the fact that the problem can be solved exactly in polynomial time, we design approximation algorithms since the performance of the exact algorithms may be too expensive for some practical applications. We present two new algorithms to compute an approximate minimum cycle basis. For any integer k≥1, we give (2k-1)‐approximation algorithms with expected running time O(kmn
1+2/k
+mn
(1+1/k)(ω-1)) and deterministic running time O(n
3+2/k
), respectively. Here ω is the best exponent of matrix multiplication. It is presently known that ω
<2.376. Both algorithms are o(m
ω
) for dense graphs. This is the first time that any algorithm which computes sparse cycle bases with a guarantee drops below the Θ(m
ω
) bound. We also present a 2‐approximation algorithm with expected running time
generated by these vectors is the cycle space of G. A set of cycles is called a cycle basis of G if it forms a basis for its cycle space. A cycle basis where the sum of the weights of the cycles is minimum is called a minimum cycle basis of G. Cycle bases of low weight are useful in a number of contexts, e.g. the analysis of electrical networks, structural engineering, chemistry, and surface reconstruction. Although in most such applications any cycle basis can be used, a low weight cycle basis often translates to better performance and/or numerical stability. Despite the fact that the problem can be solved exactly in polynomial time, we design approximation algorithms since the performance of the exact algorithms may be too expensive for some practical applications. We present two new algorithms to compute an approximate minimum cycle basis. For any integer k≥1, we give (2k-1)‐approximation algorithms with expected running time O(kmn
1+2/k
+mn
(1+1/k)(ω-1)) and deterministic running time O(n
3+2/k
), respectively. Here ω is the best exponent of matrix multiplication. It is presently known that ω
<2.376. Both algorithms are o(m
ω
) for dense graphs. This is the first time that any algorithm which computes sparse cycle bases with a guarantee drops below the Θ(m
ω
) bound. We also present a 2‐approximation algorithm with expected running time
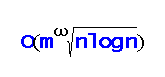 , a linear time 2‐approximation algorithm for planar graphs and an O(n
3) time 2.42‐approximation algorithm for the complete Euclidean graph in the plane.
, a linear time 2‐approximation algorithm for planar graphs and an O(n
3) time 2.42‐approximation algorithm for the complete Euclidean graph in the plane.