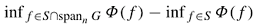Functional optimization by variable‐basis approximation schemes

Functional optimization problems arising in Operations Research are investigated. In such problems, a cost functional Φ has to be minimized over an admissible set S of d‐variable functions. As, in general, closed‐form solutions cannot be derived, suboptimal solutions are searched for, having the form of variable‐basis functions, i.e., elements of the set span n G of linear combinations of at most n elements from a set G of computational units. Upper bounds on 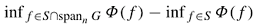$$\underset{f\in S\cap {m\mathrm{span}}_{n}G}{\inf }\Phi (f)‐\underset{f\in S}{\inf }\Phi (f)$$ are obtained. Conditions are derived, under which the estimates do not exhibit the so‐called ‘curse of dimensionality’ in the number n of computational units, when the number d of variables grows. The problems considered include dynamic optimization, team optimization, and supervised learning from data.