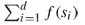Covering directed graphs by in‐trees

Given a directed graph D=(V,A) with a set of d specified vertices S={s 1,…,s d }⊆V and a function f : S→ℕ where ℕ denotes the set of positive integers, we consider the problem which asks whether there exist Σ i=1 ^d f(s i ) in‐trees denoted by $T_{i\mathrm{,1}},T_{i\mathrm{,2}},\dots ,T_{i,f(s_i)}$ for every i=1,…,d such that $T_{i\mathrm{,1}},\dots ,T_{i,f(s_i)}$ are rooted at s i , each T i,j spans vertices from which s i is reachable and the union of all arc sets of T i,j for i=1,…,d and j=1,…,f(s i ) covers A. In this paper, we prove that such set of in‐trees covering A can be found by using an algorithm for the weighted matroid intersection problem in time bounded by a polynomial in 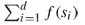and the size of D. Furthermore, for the case where D is acyclic, we present another characterization of the existence of in‐trees covering A, and then we prove that in‐trees covering A can be computed more efficiently than the general case by finding maximum matchings in a series of bipartite graphs.