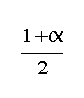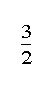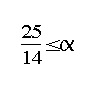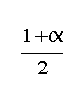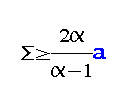We study the problem of semi‐online scheduling on 2 machines under a grade of service (GoS). GoS means that some jobs have to be processed by some machines to be guaranteed a high quality. The problem is online in the sense that jobs are presented one by one, and each job shall be assigned to a time slot on its arrival. Assume that the processing time p
i
of every job J
i
is bounded by an interval [a,α
a], where a>0 and α>1 are two constant numbers. By knowing the bound of jobs’ processing times, we denote it by semi‐online problem. We deal with two semi‐online problems. The first one concerns bounded processing time constraint. First, we show that a lower bound of competitive ratio is: (1)
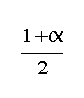 in the case where 1<α
<2; (2)
in the case where 1<α
<2; (2)
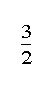 in the case where 2≤α
<5; and (3)
in the case where 2≤α
<5; and (3)
 in the case where 5≤α
<6. We further propose an algorithm, called B‐ONLINE, and prove that in the case where
in the case where 5≤α
<6. We further propose an algorithm, called B‐ONLINE, and prove that in the case where
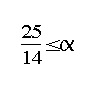 and the optimal makespan C
OPT
≥20a, B‐ONLINE algorithm is optimal. For the second problem, we further know the sum of jobs' processing times Σ in advance. We first show a lower bound
and the optimal makespan C
OPT
≥20a, B‐ONLINE algorithm is optimal. For the second problem, we further know the sum of jobs' processing times Σ in advance. We first show a lower bound
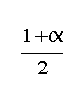 in the case where 1<α
<2, then we propose an algorithm B‐SUM‐ONLINE which is optimal in the case where
in the case where 1<α
<2, then we propose an algorithm B‐SUM‐ONLINE which is optimal in the case where
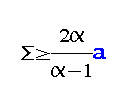 and 1<α
<2.
and 1<α
<2.