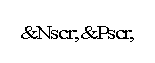We examine the performance of different subtour‐patching heuristics for solving the strongly
‐hard traveling salesman problem (TSP) on permuted Monge matrices. We prove that a well‐known heuristic is asymptotically optimal for the TSP on product matrices and k‐root cost matrices. We also show that the heuristic is provably asymptotically optimal for general permuted Monge matrices under some mild conditions. Our theoretical results are strongly supported by the findings of a large‐scale experimental study on randomly generated numerical examples, which show that the heuristic is not only asymptotically optimal, but also finds optimal TSP tours with high probability that increases with the problem size. Thus the heuristic represents a practical tool to solve large instances of the problem.
