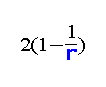The polynomial‐time solvable k‐hurdle problem is a natural generalization of the classical s‐t minimum cut problem where we must select a minimum‐cost subset S of the edges of a graph such that |p∩S|≥k for every s‐t path p. In this paper, we describe a set of approximation algorithms for ‘k‐hurdle’ variants of the NP‐hard multiway cut and multicut problems. For the k‐hurdle multiway cut problem with r terminals, we give two results, the first being a pseudo‐approximation algorithm that outputs a (k-1)‐hurdle solution whose cost is at most that of an optimal solution for k hurdles. Secondly, we provide a
 ‐approximation algorithm based on rounding the solution of a linear program, for which we give a simple randomized half‐integrality proof that works for both edge and vertex k‐hurdle multiway cuts that generalizes the half‐integrality results of Garg et al. for the vertex multiway cut problem. We also describe an approximation‐preserving reduction from vertex cover as evidence that it may be difficult to achieve a better approximation ratio than
‐approximation algorithm based on rounding the solution of a linear program, for which we give a simple randomized half‐integrality proof that works for both edge and vertex k‐hurdle multiway cuts that generalizes the half‐integrality results of Garg et al. for the vertex multiway cut problem. We also describe an approximation‐preserving reduction from vertex cover as evidence that it may be difficult to achieve a better approximation ratio than
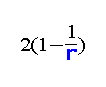 . For the k‐hurdle multicut problem in an n‐vertex graph, we provide an algorithm that, for any constant ϵ>0, outputs a ⌈(1ϵ)k⌉‐hurdle solution of cost at most O(logn) times that of an optimal k‐hurdle solution, and we obtain a 2‐approximation algorithm for trees.
. For the k‐hurdle multicut problem in an n‐vertex graph, we provide an algorithm that, for any constant ϵ>0, outputs a ⌈(1ϵ)k⌉‐hurdle solution of cost at most O(logn) times that of an optimal k‐hurdle solution, and we obtain a 2‐approximation algorithm for trees.