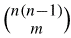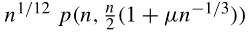We consider the 2‐XOR satisfiability problem, in which each instance is a formula that is a conjunction of Boolean equations of the form x
⊕
y=0 or x
⊕
y=1. Formula of size m on n Boolean variables are chosen uniformly at random from among all
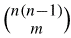 possible choices. When c
<1/2 and as n tends to infinity, the probability p(n,m=cn) that a random 2‐XOR formula is satisfiable, tends to the threshold function exp(c/2)·(1-2c)1/4. This gives the asymptotic behavior of random 2‐XOR formula in the SAT/UNSAT subcritical phase transition. In this paper, we first prove that the error term in this subcritical region is O(n
-1). Then, in the critical region c=1/2, we prove that p(n,n/2)=Θ(n
-1/12). Our study relies on the symbolic method and analytical tools coming from generating function theory which also enable us to describe the evolution of
possible choices. When c
<1/2 and as n tends to infinity, the probability p(n,m=cn) that a random 2‐XOR formula is satisfiable, tends to the threshold function exp(c/2)·(1-2c)1/4. This gives the asymptotic behavior of random 2‐XOR formula in the SAT/UNSAT subcritical phase transition. In this paper, we first prove that the error term in this subcritical region is O(n
-1). Then, in the critical region c=1/2, we prove that p(n,n/2)=Θ(n
-1/12). Our study relies on the symbolic method and analytical tools coming from generating function theory which also enable us to describe the evolution of
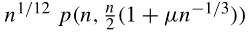 as a function of μ. Thus, we propose a complete picture of the finite size scaling associated to the subcritical and critical regions of 2‐XORSAT transition.
as a function of μ. Thus, we propose a complete picture of the finite size scaling associated to the subcritical and critical regions of 2‐XORSAT transition.