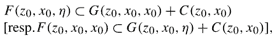| Article ID: | iaor20108145 |
| Volume: | 147 |
| Issue: | 3 |
| Start Page Number: | 607 |
| End Page Number: | 620 |
| Publication Date: | Dec 2010 |
| Journal: | Journal of Optimization Theory and Applications |
| Authors: | Lin J, Sach H, Tuan A |
| Keywords: | cone decomposition |
This paper deals with the generalized vector quasivariational inclusion Problem (P