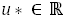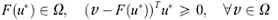Inverse variational inequalities with projection-based solution methods

An inverse variational inequality is defined as to find a vector 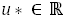$u^{*}\in {\mathbb{ℝ}}^n$ , such that 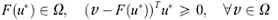$F(u^{*})\in \Omega \text{,}(v-F(u^{*}){)}^T{u}^{*}⩾0\text{,}\forall v\in \Omega \text{.}$ If an inverse function u =F ^-1(x) exists, the above inverse variational inequality could be transformed as a regular variational inequality. However, in reality, it is not uncommon that the inverse function of F ^-1(x) does not have explicit form, although its functional values can be observed. Existing line search algorithms cannot be applied directly to solve such inverse variational inequalities. In this paper, we propose two projection-based methods using the co-coercivity of mapping F. A self-adaptive strategy is developed to determine the step sizes efficiently when the co-coercivity modulus is unknown. The convergence of the proposed methods is proved rigorously.