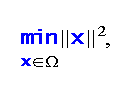Minimization of equilibrium problems, variational inequality problems and fixed point problems

In this paper, we devote to find the solution of the following quadratic minimization problem 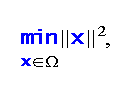$$\underset{x\in \Omega }{\min }\parallel x{\parallel }^2,$$ where Ω is the intersection set of the solution set of some equilibrium problem, the fixed points set of a nonexpansive mapping and the solution set of some variational inequality. In order to solve the above minimization problem, we first construct an implicit algorithm by using the projection method. Further, we suggest an explicit algorithm by discretizing this implicit algorithm. Finally, we prove that the proposed implicit and explicit algorithms converge strongly to a solution of the above minimization problem.