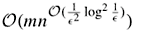Polynomial time approximation schemes for minimum disk cover problems

The following planar minimum disk cover problem is considered in this paper: given a set 𝒟 of n disks and a set ℘ of m points in the Euclidean plane, where each disk covers a subset of points in ℘, to compute a subset of disks with minimum cardinality covering ℘. This problem is known to be NP-hard and an algorithm which approximates the optimal disk cover within a factor of (1+ϵ) in 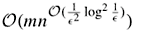${\displaystyle 𝒪\left(m{n}^{𝒪\left(\frac{1}{e^2}{\log }^2\frac{1}{e}\right)}\right)}$ n time is proposed in this paper. This work presents the first polynomial time approximation scheme for the minimum disk cover problem where the best known algorithm can approximate the optimal solution with a large constant factor. Further, several variants of the minimum disk cover problem such as the incongruent disk cover problem and the weighted disk cover problem are considered and approximation schemes are designed.