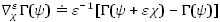Directional derivatives of oblique reflection maps

Given an oblique reflection map Γ and functions ψ χ ∈ 𝒟lim (the space of ℝ^K-valued functions that have finite left and right limits at every point), the directional derivative ∇ χ Γ (ψ) of Γ along χ, evaluated at ψ, is defined to be the pointwise limit, as ϵ ↓ 0, of the family of functions 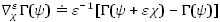${\displaystyle {\nabla }_{\chi }^{ϵ}\Gamma \left(\psi \right)\doteq {ϵ}^{-1}[\Gamma (\psi +ϵ\chi )-\Gamma (\psi \left)\right]}$ . Directional derivatives are shown to exist and lie in 𝒟lim for oblique reflection maps associated with reflection matrices of the so-called Harrison-Reiman class. When ψ and χ are continuous, the convergence of ${\displaystyle {\nabla }_{\chi }^{ϵ}\Gamma \left(\psi \right)}$ to ∇χΓ(ψ) is shown to be uniform on compact subsets of continuity points of the limit ∇χΓ(ψ) , and the derivative ∇χΓ(ψ) is shown to have an autonomous characterization as the unique fixed point of an associated map. Directional derivatives arise as functional central limit approximations to time-inhomogeneous queueing networks. In this case ψ and χ correspond, respectively, to the functional strong law of large numbers and functional central limits of the so-called netput process. In this work it is also shown how the various types of discontinuities of the derivative ∇χΓ(ψ) are related to the reflection matrix and properties of the function Γ(ψ). In the queueing network context, this describes the influence of the topology of the network and the states (of underloading, overloading, or criticality) of the various queues in the network on the discontinuities of the directional derivative. Directional derivatives have also been found useful for identifying optimal controls for fluid approximations of time-inhomogoeneous queueing networks and are also of relevance to the study of differentiability of stochastic flows of obliquely reflected Brownian motions.