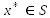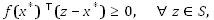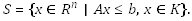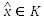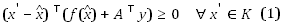Solving a class of variational inequalities with inexact oracle operators

Consider a class of variational inequality problems of finding 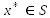${\displaystyle x^{*}\in S}$ , such that 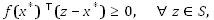${\displaystyle f\left(x^{*}{)}^{\top }\right(z-x^{*})\ge 0,\forall z\in S,}$ where the underlying mapping f is hard to evaluate (sometimes its explicit form is unknown), and S has the following structure 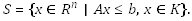${\displaystyle S=\{x\in R^n|Ax\le b,x\in K\}.}$ For any given Lagrangian multiplier y associated with the linear inequality constraint in S, a solution of the relaxed variational inequality problem of finding 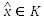${\displaystyle \hat{x}\in K}$ , such that 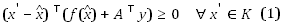${\displaystyle (x^{\text{'}}-\hat{x}{)}^{\top }(f\left(\hat{x}\right)+A^{\top }y)\ge 0\forall x^{\text{'}}\in K(1)}$ can be given by an oracle. This class of problems arises frequently in economics and engineering. In this paper, we focus on considering the above problems where the underlying mapping f, though is unknown, is strongly monotone. We propose an iterative method for solving this class of variational inequality problems. At each iteration, the method consists of two steps: predictor and corrector. At the predictor step, a trial multiplier is given and the oracle is called for a solution of the relaxed variational inequality problem (1); then at the corrector step, the multiplier y is updated, using the information from the predictor step. We allow the oracle to give just an inexact solution of the relaxed variational inequality problem at the predictor step, which makes the method very efficient and practical. Under some suitable conditions, the global convergence of the method is proved. Some numerical examples are presented to illustrate the method.