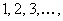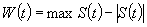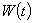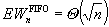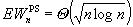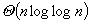The authors analyze a dynamic queue-storage problem where the arrival and departure processes are those of the single-server Poisson (M/M/1) queue. The queue is stored in a linear array of cells numbered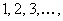 
, with at most one item (customer) per cell. The storage policy is first-fit, i.e., an item is placed at the time of its arrival into the lowest numbered unoccupied cell, where it remains until it is served and departs. Let S(t) be the set of occupied cells at time t, and define the wasted space as 
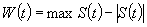, i.e. 
is the number of interior unoccupied cells. The authors analyze wasted space under the first-in-first-out and processor-sharing service disciplines. The results are expressed in terms of the ‘traffic intensity’ measure 
, i.e. the expected number in the system in statistical equilibrium. An asymptotic analysis of the steady state provides the following two tight bounds: 
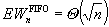and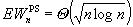
. These results are to be compared with the corresponding result, 
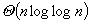, already known for the infinite server queue. In proving the new bounds, the authors also obtain estimates of the tails of the distributions of wasted space. Dynamic storage allocation in computers is an important application of the above results. The bounds show that, on average, wasted space is asymptotically a negligible fraction of the total space spanned by the queue. This in turn means that in heavy traffic time-consuming compaction (garbage collection) schemes can have very little effect on storage efficiency.
