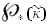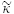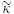| Article ID: | iaor20104861 |
| Volume: | 47 |
| Issue: | 3 |
| Start Page Number: | 329 |
| End Page Number: | 342 |
| Publication Date: | Jul 2010 |
| Journal: | Journal of Global Optimization |
| Authors: | Terlaky Tams, Ills Tibor, Nagy Marianna |
| Keywords: | interior point methods |
Linear Complementarity Problems (